Boggle Cubeset Design

Introduction

One of my summer projects for 2019 was a web-based Boggle game so that I could play with friends living in other cities. Traditional Boggle is played with physical cubes, with found words written on pen-and-paper, and each round is followed by a phase in which each player reads out the words they found, so that other players can verify the validity of those words (i.e., whether they are real words, and whether they can be found on the board) and non-unique words can be struck. This is often quite time-consuming, but one of the advantages to playing software-hosted Boggle is that this can be automated.

Sometimes, we played in French to mix things up (sidenote: my French is terrible, but it's pretty good practice). Of course, in order to still have the game track words for us at the end of each round, I needed to find a list of valid French words. I eventually found a list from ODS5, and looking through this list led me to think about how the original creators of Boggle decided what letters to paint on the faces of the cubes, and what would be a good "cubeset" for a French lexicon. I wanted to share the results of my investigations here.

Determining the Average Score of a Cubeset

The first step was to determine how to evaluate a candidate cubeset for a given lexicon (for English, I used Collins Scrabble Words 2019). Since there exists an astronomically large number of possible boards that could result from a candidate cubeset, I relied on a statistical sampling approach - "rolling" a board can be simulated by generating a random ordering of the cubes, and choosing a random face for each cube. I chose "average maximum-possible-score" as an indicator for the fitness of a cubeset to the chosen lexicon. It's worth noting that this is certainly not the only valid choice. We are assuming that a cubeset that tends to generate boards with a very high maximum possible score is desirable, but it's conceivable that someone might view sparse boards as desirable as well (if you've ever played Boggle, you will no doubt have experienced boards that are full of words and boards that seem to have no words in them... and you'll understand that those games have very different feels to them). That said, "average maximum-possible-score" (henceforth referred to as just "average score") seems like a reasonable place to begin.

I wrote up a C++ application that will generate boards for me and find all the words (github link). I tried profiling the standard 5x5 cubeset (exact cubes listed later in this post) and, 200,000 runs later (about 8 minutes on my i7-4790, although I didn't bother to make it multithreaded) out pops the following:

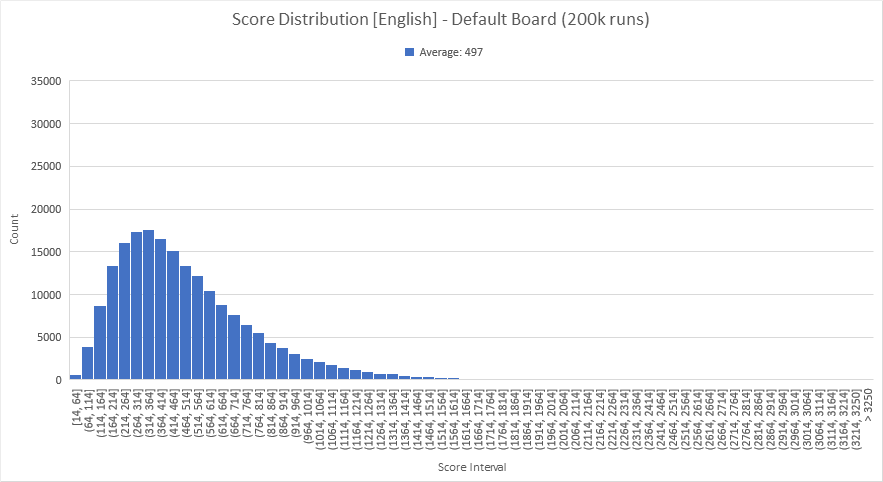
It seems we can get a fairly good idea of the average score after about 100,000 runs. The curve is not as smooth at iteration 200,000 as I would have thought, but I think we can confidently say that the average after 100,000 runs should be within ±2 of the true average score, which seems to be around 497.

Switching the Lexicon - English vs. French

So what happens if we naively switch to a French lexicon without modifying the cubes? Running another 200,000 runs showed an average score of 270. This is likely due partly to lexicon size (280k words in the English CSW19, but only 200k words in the French ODS5), but also due to the letter distribution being tailored towards the English language. We'll dive into a more thorough analysis shortly.

But first, here are some pretty charts. The two distributions look similar, but the histogram for French shows more instances with lower max scores, as expected. It's also interesting to note that, even for French, there were instances of boards where it would be possible to score well over 3000 points.

N-gram Analysis

First, let's introduce the default 5x5 cubeset. Each of the 25 strings below represents one cube, with the six letters representing a letter on each face of the cube. For the sake of alignment, the letter Q actually represents a Qu on the face of the cube. (In Boggle, Q is never alone; it is always paired with a u, which unfortunately means words like QANAT can never be scored.) How many times each letter shows up is also listed in the table below.

  AAEEEE IKLQUW DDHNOT FIPRSY DHHLOR
  CCENST OOOTUU CEIPST EIITTT GORRVW
  AAAFRS AEGMNN ENSSSU EMOTTT CEILPT
  AEEEEM DHHLNO ADENNN NOOUTW BJKQXZ
  AFIRSY AEEGMU CEIILT AAFIRS DHLNOR

Default Cubeset Letter Counts
e	19	m	4
t	13	f	4
a	12	g	3
n	11	k	3
o	11	p	3
i	10	w	3
s	9	q	2
r	8	y	2
d	6	b	1
h	6	j	1
l	6	v	1
u	6	x	1
c	5	z	1

An N-gram is a sequence of linguistic elements (here, letters) whose counts may reveal meaningful statistics about a body of text (here, the lexicon under consideration). It's not hard to imagine that the unigram counts of a lexicon should be reflected in a "good" cubeset. For example, J is the least common letter in our English lexicon, so a board that is overpopulated with J probably will not yield as many words as, say, a board that replaces some of them with S and E.

Unigrams - English Lexicon
e	287058	m	73708
s	245015	g	71315
i	229895	h	63613
a	196745	b	47310
r	177701	y	41123
n	170300	f	30331
o	168711	k	23873
t	165990	v	23418
l	133085	w	19567
c	102008	z	12279
d	85376	x	7216
u	84212	q	4301
p	76371	j	4240

Comparing these counts to the letter counts on the default cubeset, things make sense for the most part. A few departures from what I would have otherwise expected (it seems the cubeset could use a few more S, and why are there 3 W but only 1 B?), but the two tables are clearly loosely aligned.

However, since Boggle is about linking letters together to make words, the unigram counts don't tell the whole story. Let's extend N to 2, 3, and 4.

Bigrams - English Lexicon - Top 20
es	59483	st	26854
in	52550	ed	26708
er	50630	en	26189
ti	36466	ri	25637
te	30597	li	25254
ng	30357	al	25000
at	30232	an	24615
is	30071	ra	24190
re	29916	le	24138
on	29854	ne	22662

Trigrams - English Lexicon - Top 20
ing	26264	ate	8100
ati	11354	ent	7478
ess	11210	ist	6737
ion	10964	ons	6318
ers	10652	tin	6317
nes	10401	ine	6206
ies	10281	est	6164
ter	9812	ise	5616
tio	8996	ali	5607
ses	8516	tic	5503

Quadrigrams - English Lexicon - Top 20
tion	8686	ines	3036
ness	7538	ical	2884
atio	6359	over	2806
ting	4518	ring	2623
sses	4072	ment	2612
ings	4022	iest	2400
esse	3972	olog	2394
ions	3964	alis	2357
able	3168	ties	2334
ling	3080	nter	2199

(Okay, quadrigram apparently is not a word, and the concept is instead usually referred to as a "four-gram" in the literature, which seems like a real shame.)

It's worth noting at this point that our counts look drastically different from N-gram counts that you might see published elsewhere (here, for instance). If you look at bigram counts, there's a good chance you'll see TH and HE as the top bigrams for English. This is because these studies often use real English texts as their corpus, rather than a raw list of words. In those studies, the prevalence of the word "the" in the English language is enough to propel TH and HE to the top of the list (not to mention words like "that", "this", "than", etc.), whereas when we analyze our lexicon, TH doesn't even make the top 20!

A note here for Boggle players: knowing these tables will be a great help if you're hunting for large words the next time you're playing Boggle. If you see ING, ESS, or ION on the board in front of you, it may be worth spending a little extra time looking for words containing them.

Let's see what the counts look like for French. I should note that conjugations of verbs are treated as different words, as long as they are represented by a different letter sequence after accents are removed. For example, "acheter", "achetas", and "achetais" (different conjugations of "to buy") are all counted as different words, but "achète" and "acheté" are considered the same word (and are counted as if they were simply "achete").

Unigrams - French Lexicon
e	286228	d	44522
s	205335	g	30094
i	195212	f	26993
a	193894	b	26360
r	178809	z	22500
n	151284	v	20154
t	141537	h	19476
o	116867	q	9422
l	75137	x	5554
u	70659	y	5311
c	68985	j	3426
m	53717	k	646
p	47781	w	158

Bigrams - French Lexicon - Top 10
er	67360	en	45195
on	49745	ai	41748
nt	48851	es	40942
ra	48829	is	35453
re	45336	ss	33944

Trigrams - French Lexicon - Top 10
ent	31010	ion	19057
era	24892	sse	17381
ons	24675	iez	13065
ass	22390	ron	10833
rai	20641	ssi	10673

Quadrigrams - French Lexicon - Top 10
erai	15468	assi	8266
ions	14504	eron	7806
asse	12520	sion	6018
ient	9166	ment	5306
aien	8634	sent	5294

Comparing the unigram counts with English, we actually see ranking of the letters is quite similar. Notable differences are Z and Q, which are more common in French, and K and W, which are very rare in French. The differences in K and W make sense, as they are rarely used letters in French (and typically only in words borrowed from other languages).

The trigrams and quadrigrams show that a sizable percentage of words in our French lexicon come from verb conjugations. Note that the top quadrigram "erai" was seen 15468 times, whereas the top quadrigram in English "tion" was seen only 8686 times, despite the English lexicon containing 80k more words. Those with a familiarity with the French language will recognize that a large number of verbs will contribute "erai" multiple times. For example, "to buy" leads to "acheterai", "acheterais", "acheterait", "acheteraient" all being in the lexicon. Conjugations also explain the larger number of Z noted above, as almost every verb will contribute multiple words that contain "z": "achetez", "achetiez", "acheterez", "achetassiez", "acheteriez".

One final note: the n-gram analysis here treats forward and backward passes as different n-grams, in accordance with the conventional definition of the term. However, in the context of finding an n-gram in a Boggle board, there's no reason to treat them differently: if "MOOD" is on a board, then "DOOM" is also present. Therefore, perhaps a more appropriate analysis here would be to count "era" and "are" as the same trigram, etc. I ran this analysis as well, and "es/se", "ing/gni", and "tion/noit" are still the top bigrams, trigrams, and quadrigrams, respsectively, but some other n-grams do shift around. The second most frequent bigram is no longer "in/ni", but rather "er/re" which actually becomes almost as frequent as "es/se". "ess/sse" also gets a boost over "ati/ita", and "ter/ret" jumps all the way up to the fourth most frequent trigram.

Can We Do Better?

Armed with our new knowledge, let's see how much we might be able to increase the average score for English. From the default set, I tried replacing K -> S, Qu -> S, 2W -> 2R, 2C -> 2G, 5O -> 5I, 3U -> 3I, 2H -> 2N, 2H -> 2T. This is motivated largely by unigram counts presented above, but also by the other counts as well. Note that I, N, and G were all added to try to see more of those "ing" words, and various O are replaced by I because I is quite a bit more commonly found in the top trigrams and quadrigrams (I may have gone a bit overboard on this replacement, since it's not that O is uncommon, but it's a start). The changes are depicted below:

    AAEEEE IKLQUW DDHNOT FIPRSY DHHLOR
    CCENST OOOTUU CEIPST EIITTT GORRVW
    AAAFRS AEGMNN ENSSSU EMOTTT CEILPT
    AEEEEM DHHLNO ADENNN NOOUTW BJKQXZ
    AFIRSY AEEGMU CEIILT AAFIRS DHLNOR

                    ↓↓

    AAEEEE ISLSUR DDHNIT FIPRSY DNTLOR
    CGENST OIOTIU GEIPST EIITTT GORRVW
    AAAFRS AEGMNN ENSSSI EMITTT CEILPT
    AEEEEM DTNLNO ADENNN NOIUTR BJKQXZ
    AFIRSY AEEGMI CEIILT AAFIRS DHLNIR

Here are the results:

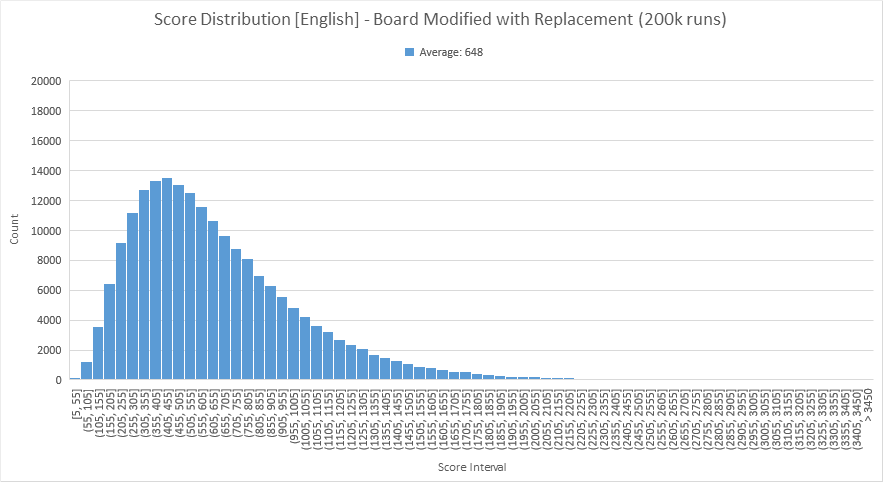
Not bad at all - average score goes from 497 to 648, approximately a 30% increase.

Let's try a different kind of change. S is somewhat special letter in English, as it is the most common pluralizing suffix. Since the plural form of a word counts as a separate word, a well-positioned S can really increase the points available on a board. So what if we rearranged letters to guarantee at least one S? From our modified board with 11 S, let's swap all of the S onto two cubes, as shown below. Bolded letters indicate letters that were swapped, but the letter distribution is unchanged here.

    AAEEEE IILIUR DDHNIT FIPRFY DNTLOR
    CGENET OIOTIU GEIPAT EIITTT GORRVW
    
ASSSSS
 AEGMNN 
SSSSSS
 EMITTT CEILPT
    AEEEEM DTNLNO ADENNN NOIUTR BJKQXZ
    AFIRAY AEEGMI CEIILT AAFIRR DHLNIR

This guarantees at least 1 S, and makes it very likely to have 2. There is a slight downside in that we miss out on ever being able to find words that end in "sses" (a common quadrigram, from words like "weaknesses", "harnesses", "obsesses", etc.), but my intution tells me this would still be a net positive change.

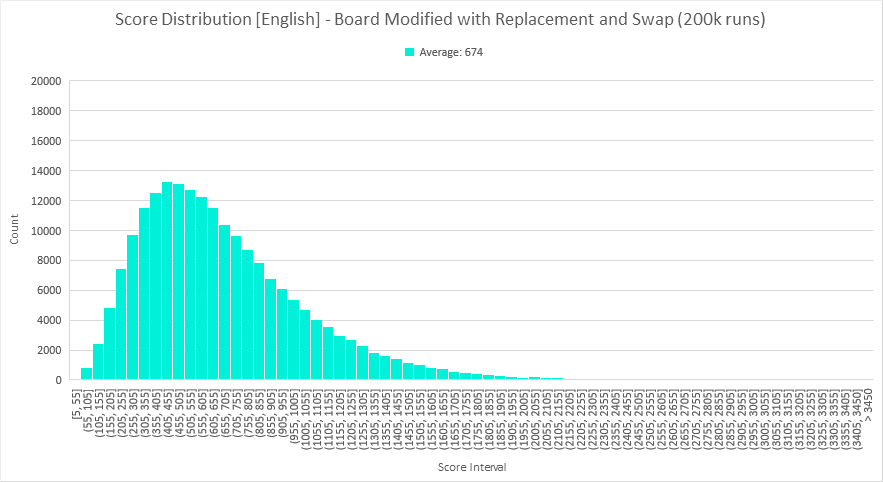
We see a smaller increase: the average score moves from 648 to 674, which is approximately 4%. I would say a 26 point increase in average score is definitely real, though, and we can conclude that the way the letters are arranged on the faces of the cube can indeed have a noticeable effect on a cubeset's potential.

What's Next?

After all of this effort to find a way to assign a numerical score to a cubeset, I'm left with one lingering thought: there is an astronomically large number of possible cubesets, but one of those cubesets must be the best, yielding a higher score than all of the others. Can we find that cubeset somehow? Moreover, can we apply that same methodology to find a better cubeset for French? Stay tuned!